The Fast Fourier Transformation and its application QA403 B75 1988
-------------------------
Online:
Wave function with fft and ifft in matlab from Physics Forum
Fourier Transform Example 2 Matlab code (a copy below)
-----------------------
Fourier Transform Example 2 Matlab code
% ***** MATLAB Code Starts Here *****
%
%FOURIER_TRANSFORM_02_MAT
%
fig_size = [232 84 774 624];
m2ft = 3.2808; % conversion from meters to feet
g = 32.2; % gravitational acceleraton (ft/s^2)
beta = 180; % relative wave direction (deg)
z = 0; % depth below the surface (ft)
rho = 1.999; % water density (lbm/ft^3)
%
w = logspace(-1,1,401); % vector of frequencies with log spacing
k = w(2)/w(1); % ratio of adjacent frequencies
delta_w = [diff(w) (k-1)*w(401)]; % differences between adjacent frequencies
w = w + delta_w .* rand(1,length(w)); % random selection of frequencies
%
H_13 = [0.1 0.5 1.25 4] * m2ft; % wave heights to be tested (ft)
%
a = 0.0081; % PM spectrum coefficients
b = 0.74;
%
for i = 1:length(H_13)
%
Upm = 12.4 * sqrt(H_13(i));
w0 = g / Upm;
%
Sa = (a*g^2 ./ w.^5) .* exp(-b*(w0./w).^4); % PM spectrum (frequency component)
%
Sb = (2/pi) * cos(beta*pi/180)^2; % PM spectrum (directional component)
%
Sc = rho * g * exp(-w.^2 * z / g); % PM spectrum (depth component)
%
S(i,:) = Sa .* Sb .* Sc; % total PM spectrum
%
end
%
%Parameters for the notch filter
%
num1 = [1 0 0.64]; den1 = [1 1.6 0.64]; % first stage numerator and denominator
num2 = [1 0 4]; den2 = [1 4 4]; % second stage numerator and denominator
num = conv(num1,num2); % total filter numerator and denominator
den = conv(den1, den2);
[mag,ph] = bode(num,den,w); % magnitude and phase of the notch filter
mag = mag'; ph = ph';
%
%Calculation of filter outputs in the frequency domain
%
for i = 1:length(H_13)
out(i,:) = mag .* S(i,:); % filter output for each sea state input
end
%
%Calculation of the time-domain wave signal for sea state 2
%and the output of that signal from the notch filter
%
t = [0: 0.125: 800]; % time vector
phi = 2*pi*(rand(1,length(w)) - 0.5); % random phase of ith frequency
A = sqrt(2*S(2,:).*delta_w); % amplitude of ith frequency
%
for i = 1:length(t)
wave(i) = sum(A .* cos(w*t(i) + phi));
wave_out(i) = sum(mag .* A .* cos(w*t(i) + phi + ph));
end
%
%Sample Fourier Transforms
%
fft_wave = fft(wave); % Fourier transform of wave signal
fft_wave_out = fft(wave_out); % Fourier transform of notch filter output
ws2 = pi / 0.125; % one-half of the sampling frequency
ww = linspace(0,ws2,3200); % frequency vector for sample Fourier transforms
[i1,i2] = min(abs(ww - 5)); % selecting the relevant frequencies
%
%Plot the data
%
figure(1),clf,subplot(211),semilogx(w,mag),grid,xlabel('Frequency (r/s)'),...
ylabel('Magnitude'),title('Notch Filter Magnitude Function'),z=axis;axis([0.1 10 z(3) z(4)]),...
subplot(212),semilogx(w,ph),grid,xlabel('Frequency (r/s)'),...
ylabel('Phase (deg)'),title('Notch Filter Phase Shift'),z=axis;axis([0.1 10 z(3) z(4)]),...
set(gcf,'Position',fig_size)
%
figure(2),clf,subplot(221),semilogx(w,S(1,:),w,out(1,:)),grid,xlabel('Frequency (r/s)'),...
ylabel('Magnitude'),title('Sea State 1 Input & Output'),z=axis;axis([0.1 10 z(3) z(4)]),...
subplot(222),semilogx(w,S(2,:),w,out(2,:)),grid,xlabel('Frequency (r/s)'),...
ylabel('Magnitude'),title('Sea State 2 Input & Output'),z=axis;axis([0.1 10 z(3) z(4)]),...
subplot(223),semilogx(w,S(3,:),w,out(3,:)),grid,xlabel('Frequency (r/s)'),...
ylabel('Magnitude'),title('Sea State 3 Input & Output'),z=axis;axis([0.1 10 z(3) z(4)]),...
subplot(224),semilogx(w,S(4,:),w,out(4,:)),grid,xlabel('Frequency (r/s)'),...
ylabel('Magnitude'),title('Sea State 4 Input & Output'),z=axis;axis([0.1 10 z(3) z(4)]),...
set(gcf,'Position',fig_size)
%
figure(3),clf,subplot(211),plot(t,wave),grid,xlabel('Time (s)'),ylabel('Height (ft)'),...
title('Wave Height, Sea State 2'),z = axis;,...
subplot(212),plot(t,wave_out),grid,xlabel('Time (s)'),ylabel('Height (ft)'),...
title('Measured Wave Height at Output of Notch Filter, Sea State 2'),axis(z),...
set(gcf,'Position',fig_size)
%
figure(4),clf,subplot(211),plot(ww(1:i2),abs(fft_wave(1:i2)),'o'),grid,xlabel('Frequency (r/s)'),...
ylabel('Magnitude'),title('Sample Fourier Transform of Wave Signal'),z = axis;,...
subplot(212),plot(ww(1:i2),abs(fft_wave_out(1:i2)),'o'),grid,xlabel('Frequency (r/s)'),...
ylabel('Magnitude'),title('Sample Fourier Transform of Notch Filter Output'),axis(z),...
set(gcf,'Position',fig_size)
%
% ***** MATLAB Code Stops Here *****

![[Packet Picture]](http://www.csupomona.edu/%7Eajm/materials/animations/packets/packet.gif)








 is
is 

 .
.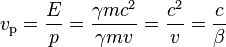

![[Maple Plot]](http://physics.usask.ca/%7Ehirose/ep225/animation/dispersion/dispersion1.gif)
![[Maple Plot]](http://physics.usask.ca/%7Ehirose/ep225/animation/dispersion/dispersion2.gif)
![[Maple Plot]](http://physics.usask.ca/%7Ehirose/ep225/animation/dispersion/dispersion3.gif)
![[Maple Plot]](http://physics.usask.ca/%7Ehirose/ep225/animation/dispersion/dispersion4.gif)


